How the Moeller Diagram Simplifies Atomic Structure Learning

Summary

Sources

psicologiaymente.comedtk.co

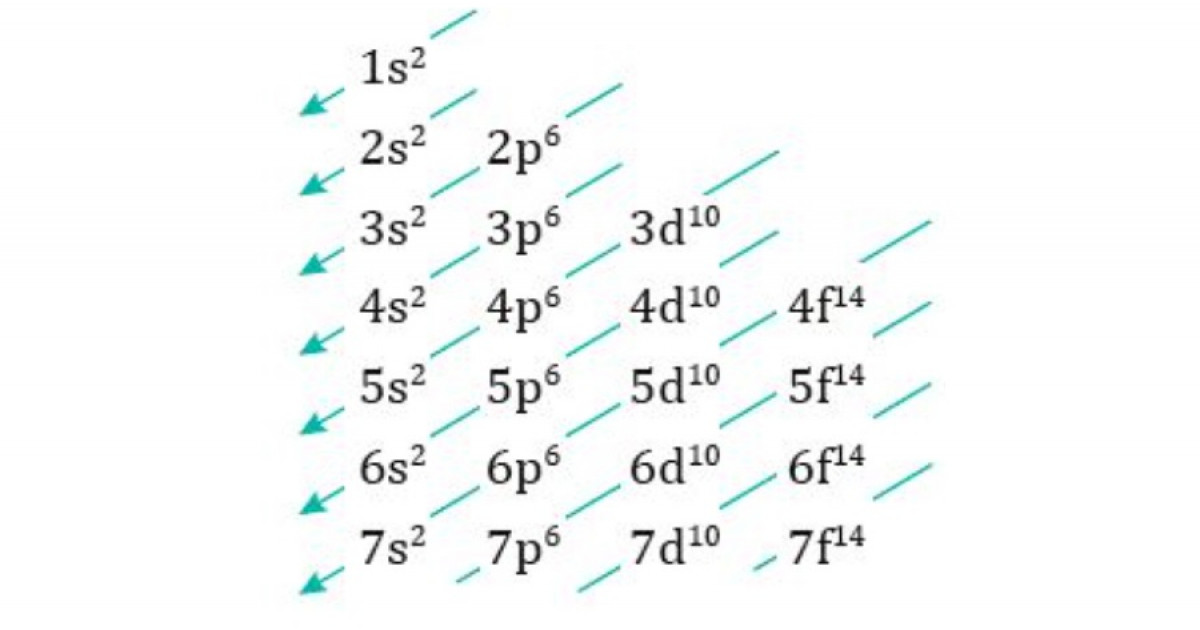
In the intricate and fascinating world of chemistry, an understanding of the atomic structure is fundamental. It is this comprehension that allows for the exploration of the behaviors and properties of elements and their interactions. One of the cornerstones of this knowledge is the electronic configuration of atoms, which dictates how electrons are distributed across different energy levels, and in turn, defines the chemical characteristics of an element. Here, we encounter the Moeller Diagram, a mnemonic graphic tool that serves as a visual aid in learning the Madelung rule, a principle that guides the order in which these electrons fill the atomic orbitals. This rule, which can at first seem daunting due to its complexity, is elegantly simplified through the use of the Moeller Diagram. The diagram itself is characterized by a series of diagonals that cut across columns representing the s, p, d, and f orbitals, in a top-to-bottom and right-to-left fashion. This creates a clear pathway for the filling order of electrons in these orbitals, governed by three quantum numbers: the principal quantum number (n), the azimuthal quantum number (l), and the magnetic quantum number (ml). To illustrate, if one were to follow the diagonals, the first would lead to the 1s orbital, the second to the 2s, the third would cross both the 2p and 3s, and so on, forming a pattern that is both predictable and reliable for most elements. The significance of the Moeller Diagram in the realm of chemistry education cannot be overstated—it transforms the abstract concepts of quantum mechanics into a visual and more tangible form, making the daunting task of memorizing the order of orbital filling far more accessible. In tandem with the Moeller Diagram is the Madelung rule, which states that atomic orbitals are filled with electrons in order of increasing n+l values, with the lowest sums being filled first. If two orbitals have the same n+l value, the one with the lower n is filled first. This rule underpins the diagram and provides the theoretical framework for why the diagram is structured as it is. However, chemistry, like any scientific field, is replete with exceptions. There are elements whose electron configurations do not adhere strictly to the Madelung rule or the predictions of the Moeller Diagram. These exceptions, often found among the transition metals and within the d and f orbitals, are attributed to the complexities of quantum interactions. Notable examples that defy these rules include chromium and copper, each possessing electron configurations that are experimentally observed to be different from the expected. Understanding the Moeller Diagram and the Madelung rule is more than academic exercise; it is a practical tool that aids in predicting the chemical behavior of elements, understanding the periodic trends, and explaining the bonding and reactivity in compounds. It stands as a testament to the synergy between visual aids and theoretical principles in the educational process, simplifying complex ideas and bridging the gap between quantum theory and chemical properties. The Moeller Diagram, colloquially referred to as the rain method or diagonal rule, stands as a graphical mnemonic that demystifies the process of determining the electronic configuration of elements. Its design is intuitive, allowing users to visualize the sequence in which electrons populate the atomic orbitals. This diagram is constructed with a matrix of cells, each representing an atomic orbital type: s, p, d, and f. These orbitals are arranged in columns, with the s orbitals forming the first column, followed by p, d, and f orbitals in their respective columns. The Moeller Diagram then employs diagonals that slash from the upper right to the lower left, across these columns, to indicate the order of electron filling. This visual representation becomes an invaluable tool for students and chemists alike, allowing for a quick reference to the often complex sequence of electron configuration. The utility of the Moeller Diagram becomes evident when one considers the three quantum numbers that define the order in which orbitals are filled. Each electron in an atom is described by these numbers, which include the principal quantum number (n), the azimuthal or angular momentum quantum number (l), and the magnetic quantum number (ml). The principal quantum number, n, indicates the energy level or shell of an electron and increases with distance from the nucleus. The azimuthal quantum number, l, differentiates the subshells or orbitals within a given principal energy level and is associated with the shape of the orbital. Finally, the magnetic quantum number, ml, which arises due to the orientation of the orbital in space, further refines the position of the electron within the subshell. In practice, the Moeller Diagrams diagonals are traced starting from the 1s orbital, moving on to the 2s, and so forth, with each diagonal leapfrogging to the next available orbital based on the Madelung rule. This rule, which is the underpinning principle of the Moeller Diagram, dictates that orbitals are filled in the order of increasing n+l values. When two orbitals have the same n+l value, the one with the lower n is filled first. Its this systematic approach that simplifies the task of determining the electron configuration of elements, without the need to memorize complex sequences or engage in trial and error. The ingenuity of the Moeller Diagram lies in its simplicity and the ease with which it translates the abstract quantum numbers into a coherent visual strategy, providing clarity and confidence in understanding the foundational aspects of atomic structure. The Madelung rule serves as a guiding principle in the filling of atomic orbitals, providing a systematic approach to understanding the arrangement of electrons around the nucleus. Central to this rule is the sum of the principal quantum number (n) and the azimuthal quantum number (l), which together determine the energy level and type of orbital that will be filled with electrons. The rule posits that orbitals with the lower sum of n and l values are filled first, reflecting the general trend that electrons will occupy the positions of lowest energy available. This is because electrons inherently seek the most stable, low-energy configurations within an atom. For example, the 1s orbital, with n equal to one and l equal to zero, will have the lowest n plus l sum of one, and is therefore the first to be populated with electrons. To illustrate the application of the Madelung rule, consider the comparison between the 3d and 4s orbitals. The 3d orbital has a principal quantum number n of three and an azimuthal quantum number l of two, giving it a sum of five. The 4s orbital, on the other hand, has an n value of four and an l value of zero, leading to a sum of four. According to the Madelung rule, the 4s orbital is filled before the 3d because its n plus l sum is lower. The second key principle of the Madelung rule addresses what happens when two orbitals have the same n plus l value. In such cases, the rule instructs that the orbital with the lower principal quantum number n will fill first. Taking the 3d and 4p orbitals as an example, both have the same n plus l value of five. However, the 3d orbital will fill before the 4p orbital because it has the lower n value, which is three compared to four for the 4p. These principles elucidate the otherwise seemingly perplexing order of electron configuration and provide an essential framework for predicting the distribution of electrons in an atom. The Madelung rule, visualized through the Moeller Diagram, brings structure and clarity to the study of atomic behavior, offering a reliable method to approach the complexities of electron configuration. Harnessing the Moeller Diagram to deduce the electronic configuration of elements begins with the atomic number, denoted as Z, which corresponds to the number of protons and, in a neutral atom, the number of electrons. By following the diagrams diagonals, one can systematically fill the orbitals in the correct order. Take Beryllium, with an atomic number of four. The first two electrons will fill the 1s orbital, as it is the lowest in energy. The remaining two electrons will then occupy the 2s orbital, following the path of the diagrams diagonals. Thus, the electronic configuration for Beryllium is 1s^2 2s^2. Moving to Phosphorus, which has an atomic number of fifteen, electrons fill the 1s, 2s, and 2p orbitals completely. The next two electrons go into the 3s orbital, and the remaining three occupy the 3p orbital, culminating in the configuration of 1s^2 2s^2 2p^6 3s^2 3p^3. Zirconium presents a more complex case with an atomic number of forty. Following the Moeller Diagram, the orbitals fill up to 4d^2 after the 5s^2 orbital, resulting in the configuration 1s^2 2s^2 2p^6 3s^2 3p^6 4s^2 3d^10 4p^6 5s^2 4d^2. Oxygen, with an atomic number of eight, follows a straightforward path until it deviates due to its common occurrence as an ion with a -2 charge, resulting in an electronic configuration that resembles Neon, 1s^2 2s^2 2p^6. Calcium, with a Z of twenty, offers an example of a cation, often forming a +2 charge in nature. Its electronic configuration as a neutral atom is 1s^2 2s^2 2p^6 3s^2 3p^6 4s^2, and as a cation, it loses the two electrons from the 4s orbital, reverting to 1s^2 2s^2 2p^6 3s^2 3p^6. However, the Moeller Diagram and the Madelung rule are not without exceptions. Chromium and Copper are classic examples where the observed electron configurations exhibit anomalies due to quantum effects and the specific stability associated with half-filled or fully filled d subshells. Chromium, for instance, with an atomic number of twenty-four, would be expected to have a configuration ending in 4s^2 3d^4. However, it prefers a more stable arrangement of 4s^1 3d^5, with a half-filled d subshell. Similarly, Copper, with a Z of twenty-nine, should theoretically end with 4s^2 3d^9 but instead adopts a 4s^1 3d^10 configuration, with a completely filled d subshell. These exceptions are indicative of the complex interplay of forces within the atom, where stability sometimes favors arrangements that do not conform strictly to the predicted order. The understanding of these exceptions is critical for a deeper insight into the subtleties of electron configuration and the behavior of atoms, transcending the predictive power of the Moeller Diagram and the Madelung rule.